이번 시간에는 다항 회귀(Polynomial Regression) 분석에 대해 알아보겠습니다.
종속 변수와 독립 변수의 관계를 2차 이상의 다항식으로 분석해야 할 때 사용할 수 있습니다.
데이터 불러오기
먼저 분석에 사용할 데이터를 불러옵니다.
깃허브에서 제공하는 시리얼 영양소 평가 데이터를 사용해 보겠습니다.
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error
import numpy as np
#%% Single variable analysis
# Data loading
cereal = pd.read_csv("https://raw.githubusercontent.com/porterjenkins/cs180-intro-data-science/master/data/cereal.csv")
데이터 전처리
데이터의 변수를 보면, 0~2열은 수치적으로 분석이 어려운 object 타입이므로 제거해 줍니다.
영양 등급(rating)을 종속 변수, 설탕함유량(sugars)을 독립 변수로 하여 분석해 보겠습니다.
# Data preprocessing
print(cereal.info())
cereal = cereal[cereal.columns[3:]]
cereal = cereal[cereal.sugars>=0]
데이터 경향 확인
몇 차의 다항식으로 분석하면 좋을지 결정하기 위해, 산점도 그래프를 먼저 그려 봅니다.
설탕함유량이 증가할수록 영양 등급이 곡선 형태로 감소하므로, 2차 다항식으로 분석해 보도록 하겠습니다.
# Scatter plot of sugars and rating
x = cereal['sugars'].values
y = cereal['rating'].values
plt.scatter(x,y)
plt.xlabel("Sugars")
plt.ylabel("Rating")
plt.show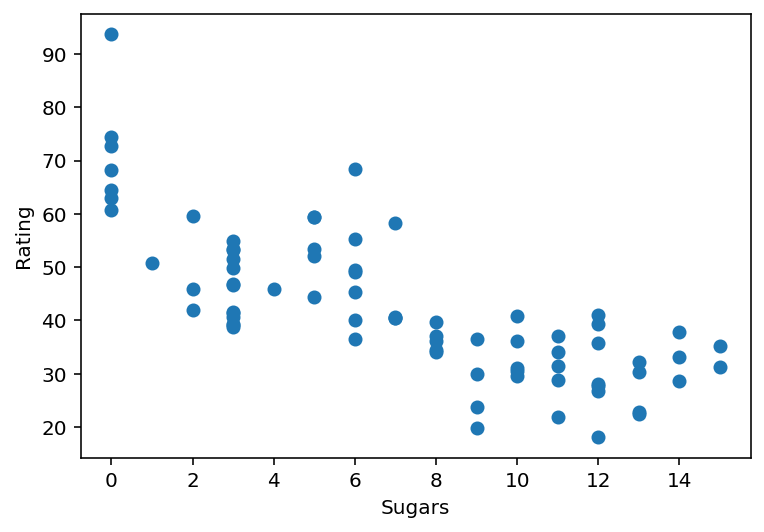
다항 회귀 모델 만들기
먼저 모델 학습 및 평가에 필요한 데이터를 준비합니다.
이때, 평가할 데이터는 전체 데이터의 30%로 하였습니다.
PolynomialFeatures 함수를 사용하여 2차 항까지 분석에 사용할 수 있게 하고, LinearRegression 함수를 사용하여 모델을 만들어 줍니다.
# Prepare train/test data
X_train,X_test, y_train, y_test = train_test_split(x,y,test_size=0.3,random_state=2)
# 2nd order polynomial regression
poly_reg = PolynomialFeatures(degree=2)
X_poly = poly_reg.fit_transform(X_train.reshape(-1,1))
reg = LinearRegression()
reg.fit(X_poly, y_train)
모델 성능 평가
predict 함수를 사용하여 영양 등급을 예측하고, pred라는 변수에 저장해 줍니다.
영양 등급의 실제값과 예측값을 그래프로 시각화할 수도 있습니다.
# Prediction
X_test_poly = poly_reg.transform(X_test.reshape(-1,1))
pred = reg.predict(X_test_poly)
# Plot real and predicted ratings
plt.figure()
plt.plot(y_test, 'ro-', label='Actual')
plt.plot(pred, 'bo-', label='Prediction')
plt.title('Rating prediction using polynomial regression')
plt.xlabel('Data index')
plt.ylabel('Rating')
plt.legend()
plt.show()
예측값이 얼마나 정확한지 수치적으로도 계산해 볼 수 있습니다.
MAE는 6.4, RMSE는 8.7, R2는 64.6 수준입니다.
# Accuracy evaluation
mae = mean_absolute_error(y_test, pred)
mse = mean_squared_error(y_test, pred)
rmse = np.sqrt(mse)
acc = reg.score(X_test_poly, y_test)
print('MAE\t{}'.format(round(mae,3)))
print('RMSE\t{}'.format(round(rmse,3)))
print('R2\t{}'.format(round(acc*100,3)))
독립 변수 개수 증가에 따른 영향
이번에는, 설탕함유량 외의 독립변수들도 사용하여 영양 등급을 분석해 보겠습니다.
독립변수를 X, 종속변수를 y로 저장하고, 모델 학습 및 평가에 필요한 데이터를 준비합니다.
이번에도 평가할 데이터는 전체 데이터의 30%로 하였습니다.
그리고 독립변수들이 여러 개이므로, StandardScaler 함수를 사용하여 변수들을 표준화해 줍니다.
X = cereal.iloc[:,:-1].values
y = cereal.iloc[:,-1].values
# Prepare train/test data
X_train,X_test, y_train, y_test = train_test_split(X,y,test_size=0.3,random_state=2)
# Normalization
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
이번에도 PolynomialFeatures 함수를 사용하여 2차 항까지 분석에 사용하고, LinearRegression 함수를 사용하여 모델을 만들어 줍니다.
# 2nd order polynomial regression
poly_reg = PolynomialFeatures(degree=2)
X_poly = poly_reg.fit_transform(X_train)
reg = LinearRegression()
reg.fit(X_poly, y_train)
predict 함수를 사용하여 영양 등급을 예측하고, 실제값과 함께 그래프를 그려서 시각화해 봅니다.
# Prediction
X_test_poly = poly_reg.transform(X_test)
pred = reg.predict(X_test_poly)
# Plot real and predicted ratings
plt.figure()
plt.plot(y_test, 'ro-', label='Actual')
plt.plot(pred, 'bo-', label='Prediction')
plt.title('Rating prediction using polynomial regression')
plt.xlabel('Data index')
plt.ylabel('Rating')
plt.legend()
plt.show()
예측값이 얼마나 정확한지 수치적으로도 계산해 보겠습니다.
MAE는 2.6, RMSE는 4.0, R2는 92.4 수준으로, 독립변수 1개를 사용했을 때 보다 예측 성능이 크게 좋아졌음을 확인할 수 있습니다.
# Accuracy evaluation
mae = mean_absolute_error(y_test, pred)
mse = mean_squared_error(y_test, pred)
rmse = np.sqrt(mse)
acc = reg.score(poly_reg.transform(X_test), y_test)
print('MAE\t{}'.format(round(mae,3)))
print('RMSE\t{}'.format(round(rmse,3)))
print('R2\t{}'.format(round(acc*100,3)))
'파이썬' 카테고리의 다른 글
| 분류분석을 통한 머신러닝 이해 (0) | 2025.05.01 |
|---|---|
| 회귀분석을 통한 머신러닝 이해 (0) | 2025.04.26 |
| 주성분 분석 (PCA: Principal Component Analysis) (0) | 2025.04.13 |
| ProfileReport : 데이터 분석을 빠르게 (2) | 2025.04.12 |
| 두 집단의 평균 차이를 통계적으로 판단 (0) | 2025.04.06 |



